How to Find Center of Parabola

The focus of the parabola is a 0 5 0. D x2 x12 y2 y12 1 12 2 22 22 42 4 16 20 25.

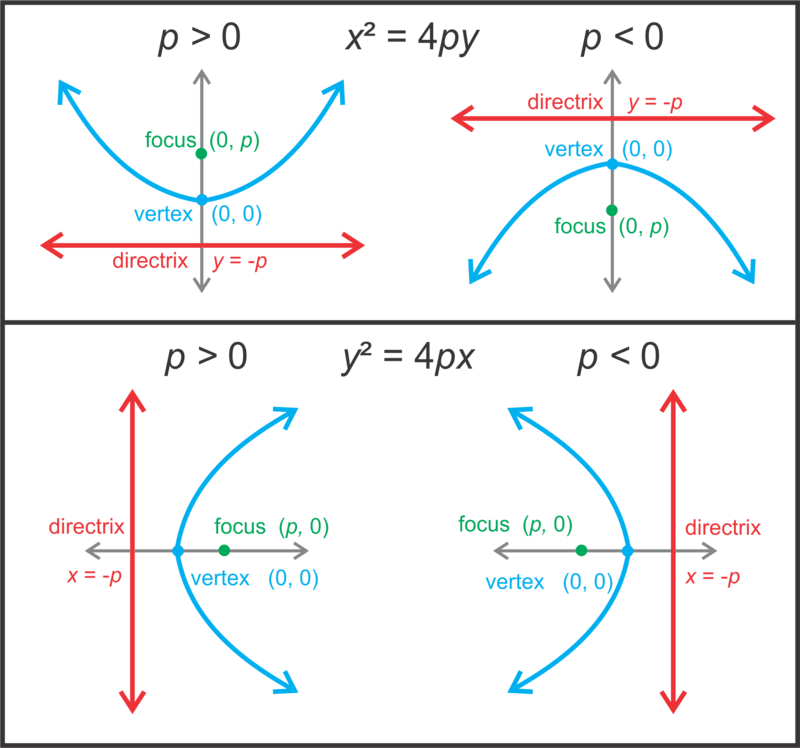
Parabolas With Vertex At The Origin Ck 12 Foundation

The directrix of parabola is x 5 0.

. So the vertex is 4 16 4 16 and we also can see that this time there will be x x -intercepts. Now from eqn 4 and 5 we have. Now that youve found the value of a substitute it into your equation to finish the example.

Learn how to graph hyperbolas. The center of the circle is on the y-axies so h0 and we substitute x1 and -x2 in the parabola equation so we can get y. 5 a 4 2 which in turn becomes.

Those two coordinates are your parabolas vertex. X 8 2 1 8 2 4 y f 4 4 2 8 4 16 x 8 2 1 8 2 4 y f 4 4 2 8 4 16. From the formula we can see that the coordinates for the focus of the parabola is h k14a.

If playback doesnt begin shortly try restarting your device. We see that the directrix is a horizontal line so the parabola is oriented vertically and will open up or down. Find the equation of the parabola whose graph is shown below.

Here are the vertex evaluations. Example 1 Graph of parabola given x and y intercepts. Up to 10 cash back y 3 x 2 12 x 12.

Partial differentiation of f xy wrt x yields -4a which can never be equal to 0. The equation is so the width of any cross section is w. Free Parabola calculator - Calculate parabola foci vertices axis and directrix step-by-step This website uses cookies to ensure you get the best experience.

By using this website you agree to our Cookie Policy. How to Find the Equation of a Parabola. Hence the equation of the parabola may be written as.

Substituting in the original equation to get the y -coordinate we get. The graph has two x intercepts at x 1 and x 2. Given the equation of parabola.

We know that because of parabolic symmetry the centre of gravity will run through the vertical line. X 2 2 -8y 3 State whether the parabola opens upward downward right or left and also write the coordinates of the vertex the focus and the equation of the directrix. Furthermore we also see that the directrix is located above the vertex so the parabola opens downward and the value of p is negative.

This will be the line that divides the parabola into two equal areas. X at2and y 2at in porometric form 1 Hence the coordinate of centre of curvature at any point x y of the parabola are 3at2 2a 2at3. Hence we need to find such that.

For the parabola having the x-axis as the axis and the origin as the vertex the equation of the parabola is y 2 4ax. X - h2 a. In this case let the equation of the parabola be represented by f xy f xy yy - 4ax where a is an arbitrary constant not equal to 0.

Determine the radius of the circle and use it to calculate its area. Take any parabola equation and find a b c values from equation. We can find the value of p using the vertex h k.

Y 3 2 2 12 2 12 24. First we find the value of h the x-coordinate of the vertex. Solution to Example 1.

The equation for a horizontal directrix is. Find the diameter using the distance formula. Where wy is found by solving the boundary equation of the parabola that was given and H is the given height of the parabola.

A 34. To graph a hyperbola from the equation we first express the equation in the standard form that is in the form. So the vertex of the parabola is at 2 24.

Well we can evaluate the axis of symmetry focus directrix vertex x intercept y intercept by using the parabola formula in the form of x y2 bx c. Notice that in this equation eqa. Frac43 y_m frac32 -frac4.

Find the equation of the parabola whose vertex is 0 0 passing through 5 2 and symmetric with respect to y-axis. We now need to find the coefficient using the y intercept at. To find the vertex of a parabola you first need to find x or y if your parabola is sideways through the formula for the axis of symmetry.

Then youll use that value to solve for y or x if your parabola opens to the side by using the quadratic equation. Here a 3 and b 12. Hence there is no centre of parabola.

Examples with Detailed Solutions. Recall that the radius of a circle is one-half of the circles diameter. Given a standard form equation for a parabola centered at h k sketch the graph.

Hence the equation of the parabola is y 2 4 5x or y 2 20x. Find the coordinates of the vertex of the parabola whose equation is eqy x2 -4x 3 eq. Equation of the parabola is y2 4ax.

Determine which of the standard forms applies to the given equation. Finding The Focus and Directrix of a Parabola - Conic Sections. So the x -coordinate of the vertex is.

Y 34 x - 12 2 is the equation for a parabola with vertex 12 and containing the point 35. Doing the x integral gives MσInt2wydy From y 1600x2 we get wy sqrty1600. In order to find the focus of a parabola you must know that the equation of a parabola in a vertex form is ya xh2k where a represents the slope of the equation.

Substitute those values in Vertex vhk. X12x12-k21 x22x22-k21 but there are three unknown so i need anothe equation i asked a teacher and he told me to find the conecation between the parabola and the two points and i do not know how to finish this question. 3 a 4 and finally.

12 2 3 2.

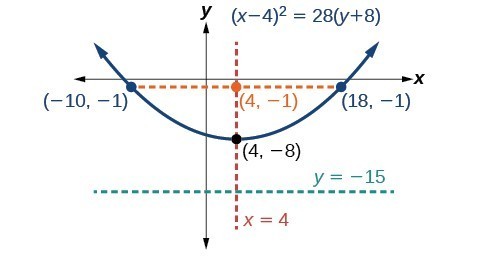
Parabolas With Vertices Not At The Origin College Algebra

Parabolas With Vertices Not At The Origin College Algebra

Parabolas With Vertex At H K Read Calculus Ck 12 Foundation